The LM Double Shadow Question
Double Shadow or reflected image?
Analysis of the double shadow in Lunar Module images
Luis E. Bilbao, PhD
1 Introduction
A double shadow of the lunar module (LM) is present in several photographs of various Apollo missions taken from inside the LM, with the source of illumination located behind the photographer in the LM. Examples from Apollo 14 can be see in Figure 1 below.
At a first glance the shadow seems to have been produced by more than one light source, or by an extended source. As the only source of illumination during the Apollo missions was the Sun, this interpretation would mean that the photographs in question were not taken on the Moon. However, it is also possible to explain the appearance of the double shadow as a manifestation of the existence of an image and a reflection. That is to say, an object and a ghost image produced by a double reflection from some of the optical surfaces. In what follows, I will try to discern whether there is a double shadow or a reflected image in the photographs of Figure 1.

Figure 1: Apollo 14. Double shadow of the LM in photographs taken from inside the module through the forward window.
Before reaching any conclusion regarding the reason for the appearance of the double shadows, we must perform a detailed analysis of the photographs since, as discussed in [1], a probable cause of this effect is a double reflection between the window and the camera. Although an inner double reflection in the window (actually a double panned window) is discarded, in principle I consider that there is no need to rule out the possible existence of reflections inside the window. Instead, what is ruled out is that the appearance of the double images is due solely to the optics of the camera, since it is not observed in any photograph that was not taken through a window.
In the case of double reflection viewed through the window, all the photos taken from inside the LM must show a double image, which should be present not only in the shadow of the LM but also in all objects present in the scene. However, there are photographs from the inside of the craft that present a double shadow with very little contrast (see Fig. 2) and others that do not have double shadows at all (see Fig. 3).

Figure 2: Apollo 12. Example where the double shadow has less contrast. Notice, also, in the photograph on the left and in the center, the appearance of a small, circular, and illuminated area, in the central part of the shadow.

Figure 3: Apollo 14. Examples without double shadow of the LM in photographs taken from inside. These were taken about 10 hours after those of Figure 1. The elevation of the Sun is greater, so the shadows are shorter.
The following sections describe the different analyses to confirm or reject the hypotheses. First, an analysis of the photographs is undertaken to obtain the characteristic(s) of the double shadows; then, an estimation of the position of the camera is made based on the known dimensions of the LM; and, based on all the transparent surfaces present in the LM, I discuss how the photographs would look in the case of a double reflection.
2 Geometry considerations
An outline of the LM and its shadow on a flat surface produced by the Sun is shown in Fig. 4. The size of the shadow depends on the elevation of the Sun above the horizon, δ, which can be obtained online using, for example, the HORIZONS Web-Interface [2]. The furthest end of the shadow, at a distance s, belongs to a point on the roof (whose height, hm, is known) that is located between the central axis of the module and its edge. The distance s is 31.1 m for photographs AS14-65-9211/4 (Fig. 1), 16.1 m for photographs AS14-64-9318/20 (Fig. 3), and 59.5 m for photographs AS12-48-7024/6 (Fig. 2).
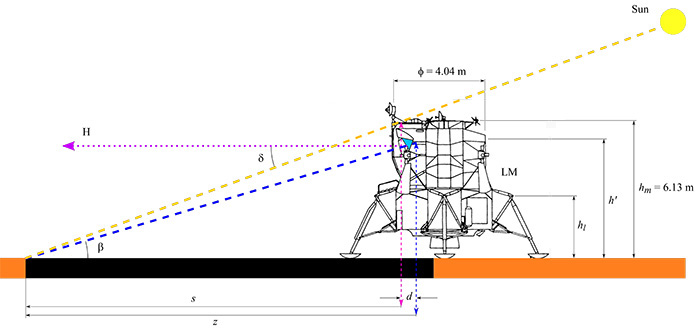
Figure 4: Diagram of the LM showing the shadow produced by the Sun on a flat surface. The diameter of the LM is φ = 4.04 m and its height hm = 6.13 m. The size of the shadow, s, depends on the elevation of the Sun above the horizon, δ. The photographs are taken at a height h', from the upper part of the window called the “forward window" (light-blue triangle) from which the shadow forms an angle β with the horizon and is at a distance z. The known height of the hinge of the legs, h1, which shadow is also visible in the photographs, helps to calibrate the distances on the surface.
The photographs were taken from the “forward window" (the light blue triangle in the aforementioned figure) from which the end of the shadow forms an angle β with the horizon. Although the exact point where each photograph was taken is unknown due to the particular geometry of this case, it is reasonable to assume that the horizontal distance d between the point of the roof that produces the longest shadow and the position where the photograph was taken, is much smaller than s, since it is, at most, of the order of half the radius of the LM (d ≤ 1 m). Thus, we can use s ≈ z, and by knowing the length of the shadow, the angular separation to the horizon, and the focal length of the camera, it is possible to determine the distances to any point of the photo as shown in Figure 5.

Figure 5: Apollo 14, image AS14-65-9211. Scale of distances on the surface, which is obtained from the length of the shadow, its angular distance to the horizon, and the focal length of the camera, assuming a flat surface.
The position and orientation of the camera in the photos can also be estimated. On the one hand, the height at which they were taken, h', follows from the fact that they were taken through the upper part of the forward window. For example, in the photograph AS14-65-9213 the horizon is seen near the upper edge of the window. Taking the center of the window at a height h = 5.35 m, we will use h' = 5.5 m. Although it is certain that d << s, to calculate the images it is necessary to have a better estimate of the distance between the window and the camera. In photos AS14-65-9212/3 we can observe part of the right and upper sections of the window frame. In addition, although very blurred, it is possible to distinguish the scale that is superimposed on the window. All this allows us to estimate the distance from the window to the camera. An average estimate distance from all photographs is d = (0.5 ± 0.2) m.
The other unknown position is the lateral displacement (with respect to the plane of the photo) between different photographs. The consequence of the lateral displacement of the camera between two photos is that closer objects have larger displacements than distant ones. From the point of view of the photographs, this is equivalent to a transformation known as “horizontal skew", see Fig. 6. Assuming that the x–axis is horizontal, the coordinates of an arbitrary point (x, y) are transformed into the coordinates (x', y') so that y' = y, and, x' - x = py + a, with p and a constants that depend on the actual displacement of the camera, ΔX, and the geometry of the problem.
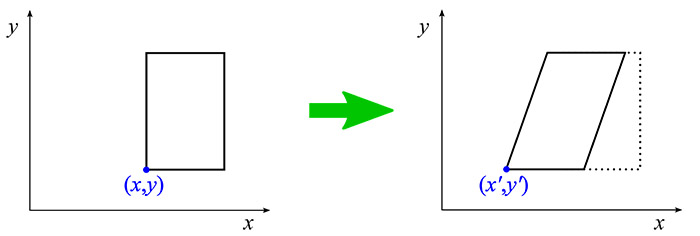
Figure 6: By moving the camera to the right, an object that appeared rectangular in a photo (left panel) is transformed in a similar way to the transformation called “horizontal skew” (right panel). Assuming that the x-axis is horizontal, the coordinates of an arbitrary point (x,y) on the photographic plate are transformed into the coordinates (x', y') such that y' = y, and x' - x = py + a, being p and a constants that depend on the specific configuration.
In the case of the photos in Fig 1, the slope of the horizontal skew can be calculated, which turns out to be p = 0.1751ΔX, where the coordinates (vertical and horizontal) are measured in mm of the photo and ΔX is the lateral displacement of the camera in meters. Using the photographs AS14-65-9213 (with the shadow on the left) and AS14-65-9214 (with the shadow on the right) with the horizontal x–axis (i.e. parallel to the horizon) the coordinates of the well-defined, small objects that appear in both photographs are measured, as shown in Fig. 7. In Fig. 8, the horizontal displacement as function of the vertical coordinate of the photo is shown, in mm. A weak dependence is observed whose slope is p = 0.0257, which implies that ΔX = 0.15 m.

Figure 7: To estimate the lateral displacement of the camera, the parallax of different objects that appear in both photos (indicated by the yellow arrows) is measured. Note that according to Fig 1 between AS14-65-9213 and AS14-65-9214 the camera is rotated on its optical axis (the horizon is seen with different inclination). For this analysis, the x-axis is chosen in the horizontal direction, namely parallel to the horizon, so this axis is seen with different inclination in these photographs.
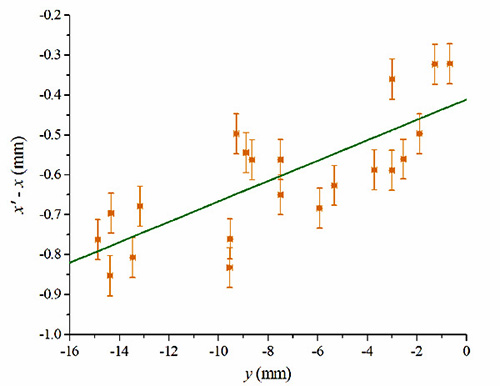
Figure 8: Lateral displacement, x' – x (in mm of the photo), of the objects detailed in Fig. 7, as a function of the vertical position, y (in mm of the photo). The best fit (green line) gives a slope p = 0.0257 which, for the present configuration, implies that the maximum displacement of the camera is ΔX ≈ 0.15 m.
On the other hand, the orientation of the camera can be divided into three movements: (a) up or down that can be measured by the angle formed by the central cross (that is, the optical axis of the camera) with the horizon, (b) left or right, which can be measured by the angle formed by the central cross with a fixed point on the surface (for example, a certain point of the shadow), and, (c) a rotation around the axis of the camera (that can be known if the horizon is visible) which due to symmetry considerations is not important for the analysis of the photos. In the photographs analyzed in this work, these orientations can be determined quite accurately.
In summary, we will consider that the camera was located within a radius of 0.2 m around a point located at a height h' = 5.5 m, corresponding to the height of the upper part of the window, at a distance d = 0.5 m away from it. As expected, lateral and up/down movements between frames were relatively small due to the limitations of the window size and the internal dimensions of the LM.
3 Shadow characteristics
To characterize the properties of the double shadow, an example of each of the situations described in the previous figures will be considered. Among the shadows that are observed with good contrast, image AS14-65-9211 is chosen as an example, Fig. 5, which is similar to AS14-65-9214 shown in Fig. 1.
The first characteristic observed in the double shadow is that the two shadows have the same apparent size. “Apparent size" means that they are of equal size in the photograph but could have different locations and size in real space. This follows from the fact that between the two shadows there is a constant separation, as seen in Fig. 9. In this case, the displacement necessary to superimpose the two shadows is 0.23 mm to the right and 2.48 mm down, which, using a focal length of the camera of 60 mm, corresponds to an angular displacement of 37.1 mrad. Note also that it is independent of the distance from the camera to the shadow (see distance scale in Fig. 9).

Figure 9: Apollo 14, detail of photo AS14-65-9211. It is observed that the two shadows have the same size and that they are displaced relatively 0.23 mm to the right and 2.48 mm down, red arrows (in mm of the photo, the distance between crosses being 10 mm). Note that this separation is independent of the actual distance in meters to the shadow measured on the ground (see blue scale).
Another feature is the dependence of the module and direction of the double shadow relative to the position of the image on the photographic plate. Fig. 10 shows the position of a similar point of the shadow in different photographs (in blue of the Apollo 12 mission and in green of the Apollo 14) together with the displacement of the double shadow indicated with red arrows.
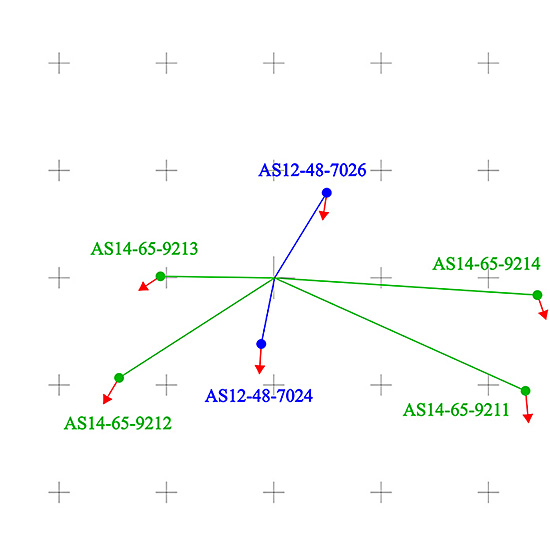
Figure 10: Position on the photographic plate of a similar point of the shadows for various photographs (in blue for Apollo 12 and in green for Apollo 14) together with the displacement of the double shadow indicated with red arrows. The distance between crosses is 10 mm. It is observed that the displacement module is almost constant, and that the horizontal displacement component has a slight dependence on the horizontal position of the point. In contrast, vertical displacement is practically independent of the position of the point.
As can be seen, both the magnitude and the vertical component of the displacement are almost independent of the position of the image in the photograph. The average value of the angular displacement magnitude of these photographs is 34 ± 2 mrad. Besides, the horizontal component of the displacement has only a weak dependence on the horizontal location of the image: the images on the right have the double shadow towards the right and vice versa for the images on the left.
In photographs AS12-48-7024 and AS12-48-7026 an illuminated area is observed within the main shadow. Expanding this area one can see a structure similar to the terrain of the rest of the photograph, see Fig. 11. This part of the land is probably illuminated by a reflection in some part of the craft’s structure, such as an antenna or other protruding structure of the main body. If the double shadows were produced by a reflected image, then this illuminated area should also have its corresponding displaced image.

Figure 11: Apollo 12, image AS12-48-7026. A bright area is observed within the main shadow. Enlarging this area (magenta circle) shows a structure similar to the background of the photograph.
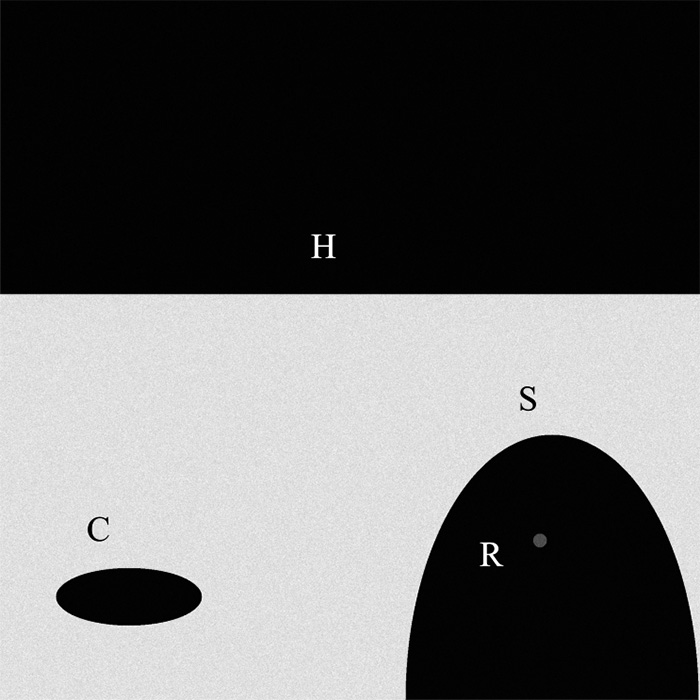
Figure 12: Simplified scheme of the shadow (S) produced by the LM on a terrain where lighting is almost uniform, contains an illuminated interior area (R), and also includes a crater (C) and the horizon (H) that marks the division of the background with the darkness of the sky.
The way that a secondary image with constant angular displacement from the original could be seen is by superimposing it with the original image which can be calculated from the simplified scheme of Fig. 12. Assuming that the reflected image has less intensity than the original image, the sum of both would produce an image like the one shown in Fig. 13.
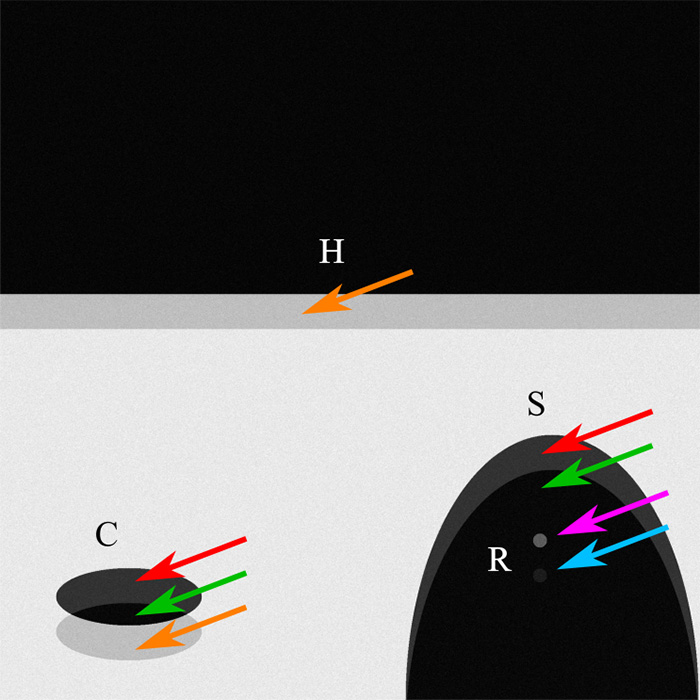
Figure 13: Superposition of the simplified scheme of Fig. 12 with a lower intensity image displaced with a constant angular displacement throughout the image. Assuming linearity between the intensity and density of the film, regions with different intensities are shown. Arrows of the same color indicate regions of equal intensity.
Four different intensity levels should be apparent for both the illuminated areas and the shadow areas (whether of the craft or the craters): a) areas where the background lighting overlaps the illuminated areas of the image (i.e., the brightest part of the picture), b) areas where the shadows in the main image overlap the bright areas in the secondary image (red arrows), c) areas where the shadows in the main image overlap the shadows in the secondary image (green arrows), and, d) areas where the illuminated part in the main image overlaps the shadows of the secondary image (orange arrows).
Although with less intensity, the bright portion inside the main shadow (magenta arrow) and the superimposition of the image of the latter and the main shadow (light blue arrow) should also be observed. To determine whether these areas are present or not in the photograph, the photographic density is measured along four lines, see Fig. 14.

Figure 14: Apollo 12, photo AS12-48-7026. It shows the four lines where the photographic density is measured. The red line is in the zone of the double shadow of the LM and also includes the illuminated zone R, the green one on the horizon, the blue one in a crater, and the orange one in another crater. For each of these lines, the origin of the x-axis is chosen at the transition point between the illuminated area and the main shadow, except on the line crossing the horizon, whose origin is chosen at the horizon itself.
In Fig. 15 the photographic density profile is shown along the green line defined in Fig. 14, which overlaps the red one, but has a different origin. The double shadow is evident in the zone with density I2, but something equivalent is not observed in the region R, which, although with different intensities and contrasts, should also present a double shadow. Nor is this double shadow present on the horizon or in the craters as can be seen in Fig. 16.
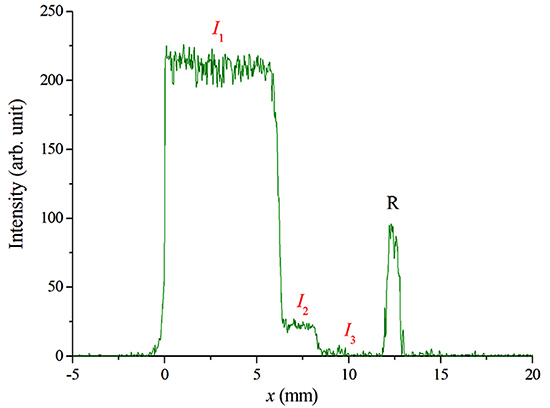
Figure 15: Apollo 12, photo AS12-48-7026. Photographic density profile along the green line (which overlaps the red one) defined in Fig. 14. From the horizon (x = 0 mm) three different sectors are observed whose average illuminations are called I1, I2, and I3. The zone I1 corresponds to the illumination of the background of the terrain, I2 corresponds to the superimposition of the intensity of the secondary image on the main shadow (which corresponds to the double shadow of the photo), and I3 to the darkest part of the shadow of the LM. Further on, the illuminated area inside the shadow is observed (region called R), which, however, does not present a transition similar to (that is, there is no double shadow or image produced by this bright spot), despite that its intensity is approximately half of I1.
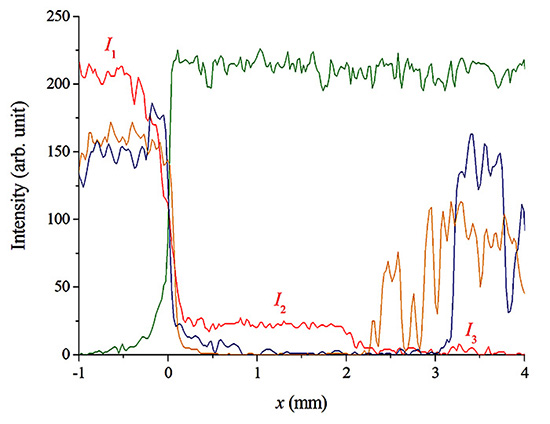
Figure 16: Apollo 12, photo AS12-48-7026. Photographic density profile along the lines defined in Fig. 14. Only on the red line does a step (I2) appear in the transition from the lighted area (I1) to the dark area (I3). Although with slightly different intensities and contrasts, this step should appear in the craters (in blue and orange), but there is only an abrupt transition between light and shadow. The absence of this step in the density profiles of the craters proves that there is no double shadow or image of them. Nor is there a double image on the horizon (green line) that has a jump of opposite intensity (it goes from shadow to light), since from the horizon the intensity is practically constant.
The transition between the main and secondary shadow, which is observed in the red line as an intermediate density step, I2, is not observed. Neither on the horizon (in green) nor in the craters (in blue and orange) where there is an abrupt transition between shadow and light or light and shadow.
It can be argued that in the process of scanning and publishing on the internet, the color or gray scales could have been modified and, therefore, those transitions were lost. This argument could be valid on the horizon and below the craters (see orange arrows in Fig. 13) where the contrast is weaker, but not in the main shadows of the craters (green and red arrows) that have intensities practically equal to the shadow of the LM.
4 About reflections
Since the forward window is composed of two panels [3] there is a possibility that the double shadow is produced by a spurious image reflected in the panels (or even, in some optical element of the camera), so therefore all possible ways for the occurrence of these reflections must be studied. In this interpretation, what we see in the photographs would be the superposition of the main image with a reflected image, as shown schematically in Fig. 17. Only a double reflection will be considered, since the intensity of any successive reflections decay and therefore cannot be detected.
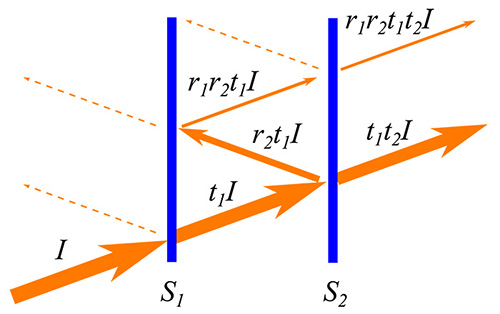
Figure 17: After crossing the surfaces S1 and S2 the intensity, I, of a beam is reduced to t1t2I since it has partly been reflected and the rest has been transmitted (t1 and t2 are the surface transmission coefficients 1 and 2, respectively). The first reflection in S1 is lost (to the left, dotted line), but the reflection in S2, with intensity r2 t1 I (r2 is the reflection coefficient of S2), can be reflected again in S1 (with coefficient r1) and, in this way, continue through S2. The final intensity through this path is r1r2 t1t2I. This leads to the fact that the ratio of intensities between the beam that suffered the double reflection with respect to the beam that crossed the two surfaces is r = r1r2, that is it only depends on the coefficient of internal reflection of surfaces.
As shown in Fig. 17, after crossing the surfaces S1 and S2 a beam of intensity I has its intensity reduced to t1t2I since it has been partly reflected (t1 and t2 are the transmission coefficients of surfaces 1 and 2, respectively). The first reflection in S1 is lost (to the left, dotted line), but the reflection in S2, with intensity r2t1I (r2 is the reflection coefficient of S2), is reflected in S1 (with reflection coefficient r1) and, thus, continue through S2. The intensity of this double reflection is r1r2t1t2I. The relation of intensities, r, between the beam that suffered the double reflection and that of the beam directly transmitted across the two surfaces is r = r1r2, that is, it only depends on the internal reflection coefficients of the surfaces.
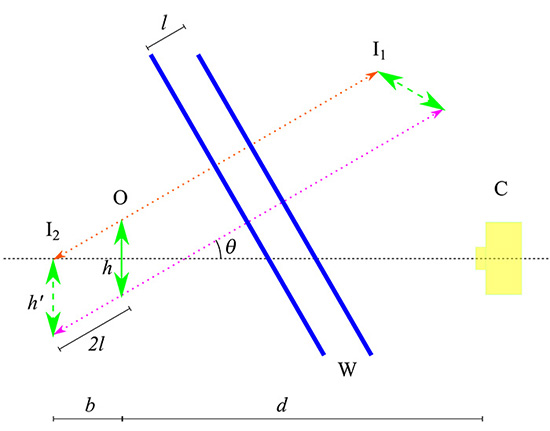
Figure 18: Scheme of two flat parallel surfaces (blue lines). Given an object, O, the first image, I1 (produced by the second surface), is in a direction perpendicular to the surfaces, and its second reflection, I2 (on the first surface), is located at a distance 2l behind the object, also in the direction perpendicular to the surfaces (l is the separation between the surfaces). As can be seen, the linear magnification is 1, since h' = h. However, the angular magnification seen from the camera is less than 1 since I2 will always be farther than O.
As mentioned above, this double reflection leads to the formation of several zones of different intensity, which allows us to estimate the value of r. Assuming that there are only two levels of intensity: I the mean intensity of the background and Is the intensity of the shadow, and that there is a double image produced by reflection, from the definitions in Fig. 15, it follows that I1 = I (1 + r) because it is the superposition of the illuminated areas of the image and its reflection, that I2 = Is + r I, because it is the sum of the main shadow and the illuminated area of the reflection, and that I3 = Is (1 + r), because it is the sum of the main shadow and its own reflection. From these relationships we get
![]()
Using average values along the green line of Fig. 15, we have I1 ≈ 210.14, I2 ≈ 22.44, and I3 ≈ 2.19, so that r ≈ 0.108. As this is the product of the reflection coefficient of two surfaces, on average each of them has a coefficient r1 ≈r2 ≈ 0.329, which is very large for a transparent surface. Of course, this is valid if linearity is assumed between the intensity of the light and the photographic density of the photograph published on the internet. This implies that in order to estimate a realistic value, it would be necessary to consider not only the response of the photographic emulsion, but also the process of digitization and the intensity and contrast corrections that may have been done to the photographs for publication. But whatever the process would have been, the same original intensity of the light should correspond to the same photographic density and vice versa.
5 Image formation
For the formation of a secondary image there are two possibilities: (a) that there is a double reflection between the two panels of the window, or (b) that the double reflection occurs between a panel of the window and some optical surface of the camera. In the first case, the first option is to study the case of two parallel flat plates, Fig. 18, since it corresponds to the geometry of the forward window [3]. But it can also be considered that the plates are not strictly parallel, Fig. 19.
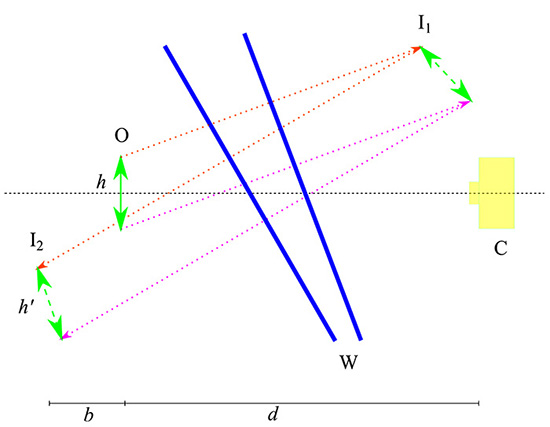
Figure 19: Scheme of two non-parallel flat surfaces (blue lines). The analysis is similar to the case of parallel surfaces, Fig. 18. Image I2 will be formed behind O, the linear magnification is 1 (h' = h) and the angular magnification is less than 1 as seen from the camera, C. The main difference is that the image I2 will be angularly offset with an angle proportional to that formed between the two surfaces.
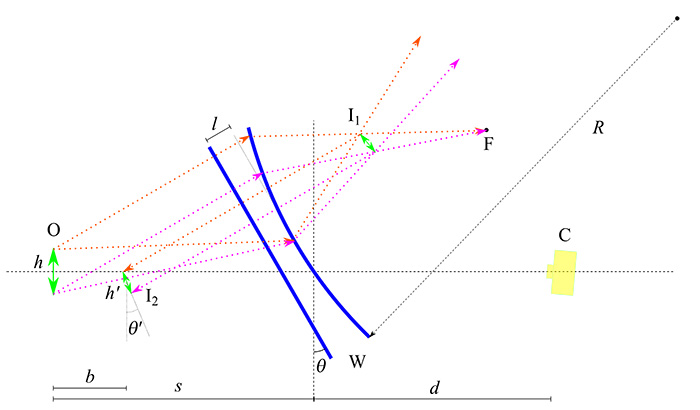
Figure 20: Scheme of a flat surface and a curved surface (blue lines). The analysis in this case is more complex than in the previous cases, since it depends strongly on the radius of curvature, R, of the curved surface. When R – ∞ the previous results for two flat surfaces are recovered. At the other end, when R << 1, a small image is obtained (h' << h) located near the first window (in this case, b is comparable to s). Among these cases there are many different solutions.
On the other hand, in the second case, a possibility is the reflection on some flat surface of a filter or protection that could exist in front of the objective (magenta dotted line in Fig. 21), or the reflection on the spherical surface of the first lens of the objective (blue curve in Fig. 21). The study of these latter cases is similar to the first ones, with the difference that, now, the second surface cannot be considered as fixed since it moves with the camera, both spatially and angularly.
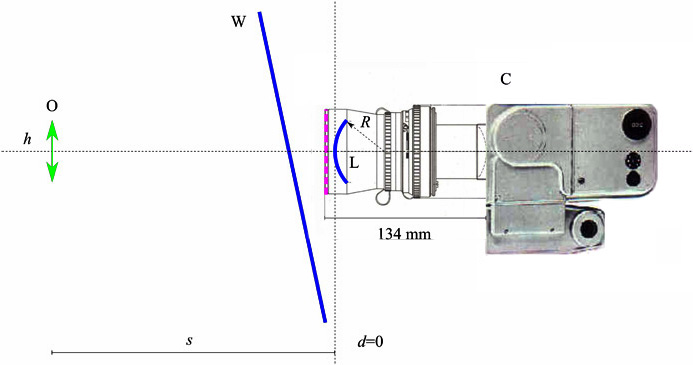 Figure 21: In addition to the possible double reflection between the two panels of the forward window the case of a double reflection between a window panel, W, and an optical surface of the camera, C, can be studied. One possibility is the reflection on the surface of the first lens, L, (blue curve) of the camera objective, whose radius of curvature, R, is known (in the case of the Zeiss Biogon 5.6 lens, it is R ≈ 40 mm) [4]. The other possibility is a reflection on some flat surface of a filter or protection that could exist in front of the target (magenta dotted line). The study of these cases is similar to the previous ones, with the difference that now the second surface cannot be considered fixed as it moves with the camera, both spatially and angularly.
Figure 21: In addition to the possible double reflection between the two panels of the forward window the case of a double reflection between a window panel, W, and an optical surface of the camera, C, can be studied. One possibility is the reflection on the surface of the first lens, L, (blue curve) of the camera objective, whose radius of curvature, R, is known (in the case of the Zeiss Biogon 5.6 lens, it is R ≈ 40 mm) [4]. The other possibility is a reflection on some flat surface of a filter or protection that could exist in front of the target (magenta dotted line). The study of these cases is similar to the previous ones, with the difference that now the second surface cannot be considered fixed as it moves with the camera, both spatially and angularly.
In the case of the reflection in the parallel plates of the window, Fig. 18, given an object, O, the first image, I1 (produced by the second surface), is in a direction perpendicular to the surfaces, and its second reflection, I2 (which occurs on the first surface), is located at a distance 2l behind the object in the direction perpendicular to the surfaces (l is the separation between the surfaces). As can be seen, the linear magnification is equal to 1, since h' = h. However, the angular magnification, M∝, as seen from the camera is less than 1 since I2 will always be farther away than O. This behavior can be estimated as follows. Let Ø be the angle between the axis of the camera and the normal to the window, d the distance of the object from the camera, and b the component of 2l along the direction of the camera, that is,
![]()
Since there is no linear magnification (h' = h), the angular magnification, M, is calculated from
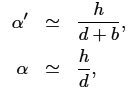
(a is the angular size of the object and a' that of the image) so that
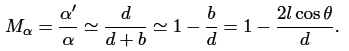
On the other hand, the linear displacement between the object and the image, Δy, is
![]()
while the angular displacement, Δμ, is
![]()
This implies that the displacement observed in the photographic plane is
![]()
where f is the focal length of the camera.
As an example, we can put Ø = 30 deg, l = 0.05 m and d = 30 m which gives Δy' = 0.1 mm (that is, one hundredth of the separation between crosses of the reticulate) and Δμ = 1.67 mrad which is much smaller than 34±2 mrad observed in the six cases mentioned. To obtain a displacement such as that measured in the photographs, that is ≈ 30 mrad, a separation of the two panes of the window, l, of about 1 m, would be necessary, which is impossible for a window of the LM.
In addition, the separation between the object and the image on the plane of the film would be inversely proportional to the distance, contrary to what is observed (non dependence on the distance). In nearby objects the effect should be very noticeable, but it is not observed in the photographs. Through more precise simulations for the calculation of the image, which do not use the approximations above, these results are confirmed, which discards the double reflection in the parallel flat plates of the window.
It could be assumed that the plates are not exactly parallel, Fig. 19. In this case, the angular displacement of the image is twice that of the angle formed between the plates. To form a displaced image of about 34 mrad, the angle between panels should be about 17 mrad (≈ 1 deg). In Fig. 22 the separation between the object and the image is schematically shown.
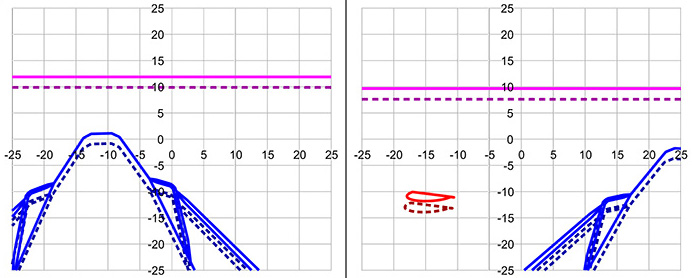
Figure 22: Scheme of the simulation of a double image produced by double internal reflection between the panels of the “forward window” assuming that the plates are flat but their normals differ by an angle of 1 deg (≈ 17.45 mrad). Using the parameters calculated in Section 2, the simulations of photos AS14-65-9213 (left panel) and AS14-65-9214 (right panel) are shown. The horizontal and vertical scales of the photo are in mm. The outline of the shadow of the LM is represented in blue, that of the horizon in magenta, and that of a crater in red. Solid lines refer to the main image and dashed lines to the secondary one. It is observed that the double shadow of the LM is fixed and independent of the location and orientation of the camera, contrary to what was observed. In addition, the existence of the double image of the horizon and craters that are not observed in the photos are predicted.
As can be seen, the double shadow of the LM would be fixed and independent of the location and orientation of the camera, contrary to what is observed. In addition, the existence of the double image of the horizon and the craters, that are not observed in the photos, is predicted. It should be noted that with angles greater than 1 deg a greater displacement would occur, larger than that observed. Therefore, it should be ruled out that the double shadow is the product of a double image between the panels of the forward window.
In the case of a possible double reflection between the window and some filter or flat protection that is in front of the camera lens, the image formation is similar to the case of the non-parallel plates, Fig. 19, but it should be considered that the second surface changes orientation along with the camera. The simulations show that the images have large displacements (much larger than those observed), since they accompany the rotation of the camera, even to the point of being outside the visual field of the photo, in particular for cases AS14-65-9213/4. This rules out this kind of double reflection.
Finally, there is the possibility that there is a double reflection between the forward window and the spherical surface of the first optical element of the objective. Using the radius of curvature of the spherical surface is R = 40 mm [4], the simulations of photos AS12-48-7024 (left panel) and AS12-48-7026 (right panel) are shown in Fig. 23.
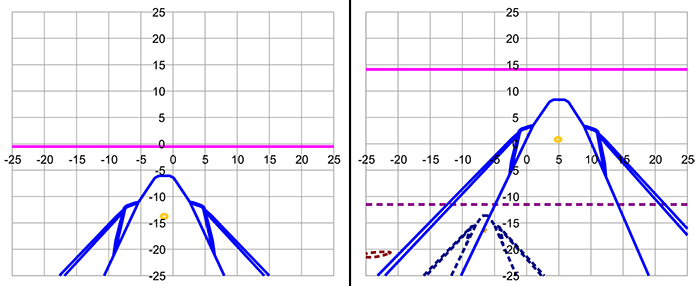
Figure 23: Scheme of the simulation of a double image produced by double reflection between the forward window and the spherical surface of the first optical element of the objective. Using that the radius of curvature of the spherical surface is R = 40 mm, the simulation of photo AS12-48-7024 (left panel) and AS12-48-7026 (right panel) is shown. The horizontal and vertical scales of the photo are in mm. The outline of the shadow of the LM is represented in blue, that of the horizon in magenta, and the illuminated area within the shadow in yellow. Solid lines refer to the main image and dashed lines to the secondary one. A reduced image is obtained and its position changes strongly with the location and orientation of the camera, since the displacement of the secondary image is proportional to the angle of rotation of the camera, which is ≈ 14 deg between the two photos. In fact, in the left panel, the secondary image is out of the visual field of the camera. In addition, as in the previous case, the double image of the horizon and craters that are not observed in the photos are predicted.
The horizontal and vertical scales are in mm of the photo. In blue the outline of the shadow of the LM is represented, in magenta that of the horizon, and in yellow the illuminated area within the shadow. Solid lines refer to the object and dashed lines to the image. It can be seen that a reduced image is obtained and that its position changes markedly with the location and orientation of the camera, because the displacement of the image is proportional to the angle of rotation of the camera, which is ≈ 14 deg between the two photos. In fact, in the left panel the reflection is outside the visual field of the camera. In addition, as in the previous case, the double image of the horizon and craters is predicted, but not observed in the photos.
In summary, these analyses show that the observed double shadow cannot be due to an image formed by reflection between the flat panels of the window (whether parallel or not), nor by a reflection between a window panel and an optical element of the camera.
6 Deformed window
Given that the above options do not lead to the explanation of the presence of the double shadow, it is possible that the inner plate of the window is curved due to the difference in pressure between the interior of the LM and the exterior. From the photos, after doing numerous simulations with different radii of curvature, the solution that best reproduced the characteristics of the double shadow was sought. As expected, a very large radius of curvature (greater than the distances involved) led to results similar to that of flat plates, whereas a very small one gave very small images, as in the case of reflection on the first surface of the objective. That is why we investigated the range of radii of curvature from a meter to tens of meters.
Fig. 24 shows the simulation of the image produced by double reflection in the panels of the forward window assuming that the external panel is flat and the internal one is convex with a uniform radius of curvature R = 5 m. Using the parameters of the position and orientation of the window and camera discussed in Section 2, the case of photo AS14-65-9213 (left panel) and that of AS14-65-9214 (right panel) is shown. The double shadow of the LM is relatively well reproduced in both cases, but a double image of the horizon and of the craters, that is not observed in the photos, is also predicted.

Figure 24: Simulation of a double image produced by double reflection in the panels of the forward window assuming that the external panel is flat and the internal one is convex with uniform radius of curvature (a naive approximation of a deformed window due to the inner pressure of the LM). Using the parameters calculated in Section 2, the simulation of photo AS14-65-9213 (left panel) and AS14-65-9214 (right panel) is shown. The double shadow of the LM is reproduced relatively well in both cases, but the double image of the horizon and of the craters that are not observed in the photos are also predicted.
Further, the hypothesis of uniform radius of curvature can only apply to a central region of the window. In an actual deformed window the curvature changes from concave to convex near the frame of the window. Therefore the displacement between shadows will vary, contrary to the observed uniformity in the photographs.
Also, for the Apollo 12 photos (Fig. 25, the left panel corresponds to AS12-48-7024, and the right panel to AS12-48-7026) the simulation of a double image reproduces fairly well the shadow of the LM in both cases, but again, there should be double image of the horizon and craters, a fact that is not observed in the photos.

Figure 25: Simulation of a double image produced by double reflection in the panels of the forward window assuming that the external panel is flat and the internal one is convex with uniform radius of curvature (a naive approximation of a deformed window due to the inner pressure of the LM). Using the parameters calculated in Section 2, the simulation of photo AS12-48-7024 (left panel) and of AS12-48-7026 (right panel) is shown. The double shadow of the LM is reproduced relatively well in both cases, but the double image of the horizon and of the craters that is not observed in the photos is also predicted.
Further, the hypothesis of uniform radius of curvature can only apply to a central region of the window. In an actual deformed window the curvature changes from concave to convex near the frame of the window. Therefore the displacement between shadows will vary, contrary to the observed uniformity in the photographs.
Due to the response of the film, and/or the scanning process, and/or the settings for its publication on the internet, there may be tones that look the same even though they were originally different. But whatever the process would have been, the same original intensity should correspond to the same photographic density, so the double shadow of the crater should be equally visible as that of the LM. However, only the shadow of the LM is observed in the photos. In Fig. 26 the existence of a double shadow is observed in the contour of the shadow of the lunar module (blue arrows) but not around other objects or shadows that, due to their almost zero illumination (similar to the shadow), should also present double image or shadow (yellow arrows).

Figure 26: Photographs showing the existence of a double shadow around the shadow of the LM (blue arrows) but not around other objects or shadows that, due to their almost zero illumination, should also present a double image or shadow (yellow arrows).
This is also seen from the intensity profile obtained from the simulation of photo AS12-48-7026 (right panel of Fig. 25), shown in Fig. 27.
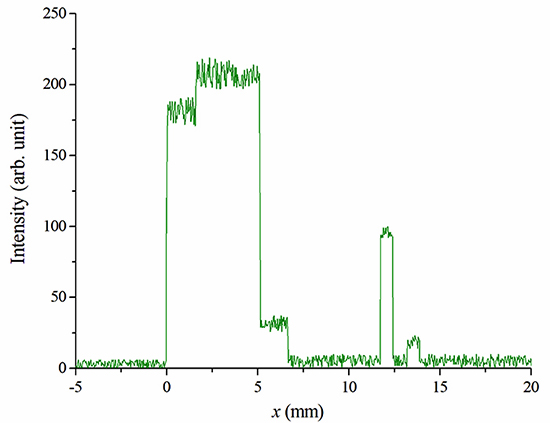
Figure 27: Intensity profile obtained from the simulation of photo AS12-48-7026, see right panel of Fig. 25. The simulation uses a background intensity with slight variations to reproduce the lighting variations of the objects present on the surface. The horizon corresponds to x = 0. From there a first step is observed that corresponds to the double image of the horizon (which is not observed in the measured intensity, Fig. 15), followed by an almost constant intensity of the background and the transition to the darkest part of the shadow.
The simulation uses a variable intensity of the background to reproduce the intensity variations that appear in the photograph due to the irregularity of the surface and the presence of stones of different sizes. The horizon corresponds to x = 0. From there, a first step is observed that corresponds to the double image of the horizon (which is not observed in the measured intensity, Fig. 15), followed by an almost constant intensity of the background and a second step from the transition to the darkest part of the shadow. This second step corresponds to the double shadow, as observed in the measured intensity, Fig. 15. Finally, the peak corresponding to the illuminated area within the main shadow is seen along with its reflection, which is not observed in the photography.
In addition, comparing Fig. 27 with Fig. 15, it is observed that the expected density steps are larger than fluctuations due to the irregularity of the terrain, and therefore, regardless of the brightness and contrast adjustment of the photos, those steps should be present in the photographs (because otherwise the fluctuations would have disappeared), but they have not. This again shows that the double shadow is not due to an image produced by double reflection, since only the LM has this double shadow and only around its contour, but not inside where the small lighted area is, nor anywhere else in the photography.
Finally, a detail of the lower right part of the photo AS14-65-9213 is shown in Fig. 28. The red arrow indicates the double shadow, while the blue one indicates the edge of the window. The distance between the two, measured on the plane of the window is c < 0.1 m.

Figure 28: Detail of the lower right part of the photo AS14-65-9213. The red arrow indicates the double shadow, while the blue arrow indicates the edge of the window. The distance between the two, measured on the plane of the window, is c < 0.1 m.
If the double image was due to the curvature of the window (for the internal pressure of the LM), a radius of curvature of 5 m at less than 0.1 m from the frame, would require a large deformation in the central part of the window. An estimate of the deformation of the internal window panel can be made from the size of the triangular window (≈ 25 inch side), the pressure difference across the panel (≈ 1/3 atm), the thickness of the panel (≈ 1/4 inch), Young’s modulus (≈ 71.5 GPa), and Poisson ratio (≈ 0.21) of the glass. Under these conditions, the minimum radius of curvature in the center of the glass would be 17 m, that corresponds to a deformation three times smaller than that necessary to reproduce the images, and about R = 60 m at 0.1 m from the edge. Further, closer to the edge, the curvature changes from convex to concave. The distortion of the image in this region would be very noticeable. Therefore, the window distortion cannot reach the required radius of curvature, nor reproduce the uniformity of the double shadow.
7 Conclusions
In this work I studied the possibility that the double shadow observed in some photos of the Apollo missions was a spurious image produced by reflections between the window panels, or between a panel and some optical element of the camera.
The reflection between a window panel and the camera is discarded because the secondary image should move proportionally to the camera movement between different photographs, that is, tens of degrees in the analyzed photographs, but only displacements of no more than about one degree are observed. In addition, if the reflection was on the convex surface of the first lens of the objective, which has a rather small radius of curvature, the secondary images would also be small, contrary to what is observed: the main and secondary images are of equal size.
The separation of the shadow does not depend on the distance. The internal reflection between the flat surfaces of the forward window cannot explain the shift of the shadow with the position and orientation of the camera, and cannot explain the value of the angular separation (except in the case where the angular separation between surfaces is approximately 1 deg).
The last possible option is the formation of an image assuming the deformation of the internal window panel. A solution close to what is observed requires a very large deformation (that is, a fairly small radius of curvature) even near the window frame where the deformation is expected to be small. In addition, the required curvature seems impossible to be achieved with a pressure difference of 1/3 atm in a triangular window of about 25 inches on the glass used in the Apollo missions. Further, the change of curvature from convex to concave that takes place near the edge, would distort the image in a manor that is not observed.
In addition to these arguments, the most surprising and inexplicable fact is that the double image is only observed on the edge of the shadow of the LM. There are no indications of a secondary image either on the horizon, or inside the main shadow (as shown by the small illuminated area), not in craters that have an intensity level similar to the shadow of the LM, nor in the image of the rocket engine, which is located close to the window, in the shadow of the LM.
All this leads to the certainty that the double shadow observed (only in the contour of the shadow of the LM) is not an image produced by reflections, under the conditions of the Apollo missions. Because of the characteristics described throughout this work, it is most likely that the double shadow is precisely that: a double shadow produced by two light sources angularly separated by about 35 mrad. The step-wise transition between light and shadow rules out an extended light source. Also, we can discard the Sun as extended source, because its angular diameter is about 10 mrad. What is not in agreement with this possibility is the presence of craters or irregularities of the terrain, immediately next to the main shadow, that seem to be duplicated within the second shadow.
But regardless of the possibilities of what the double shadow could be, what can be affirmed is what it is not. The double shadow is not produced by reflections from any optical surfaces present in the Apollo missions.
Luis E Bilbao
Aulis Online, December 2019
Addendum, February 2020 read here
References
[1] https://space.stackexchange.com/questions/37154/why-are-there-double-shadows-in-this-apollo-14-magazine (accessed Sep. 22, 2019).
[2] https://ssd.jpl.nasa.gov/horizons.cgi (accessed Sep. 22, 2019)
[3] https://www.lpi.usra.edu/lunar/documents/apolloSpacecraftWindows.pdf (retrieved Sep. 25, 2019)
[4] https://www.hq.nasa.gov/alsj/Biogon5.6_60mm_ZEISS.pdf (retrieved Sep. 19, 2019).
About the Author
Luis Ernesto Bilbao has a PhD in Physics from the University of Buenos Aires, is Adjunct Professor, and Independent Researcher, INFIP CONICET, UBA (the Faculty of Exact and Natural Sciences, University of Buenos Aires, Argentina).
The Institute of Plasma Physics (INFIP), dependent on the CONICET and the FCEyN-UBA, is a center carrying out pure and applied research in a wide variety of subjects of this discipline. The INFIP researchers have extensive knowledge and many years of experience in this branch of physics, with the publication of more than 600 works since 1983.
AULIS Online – Different Thinking