Apollo 14: Second Light Source Confirmed
Background
It has been said that if just one single lunar surface photograph allegedly taken during an Apollo mission was proven to be a fake image, then the entire mission record would be called into question. Here, a monochrome photograph taken during Apollo 14, AS14-68-9486 is investigated further.
Way back in the 1990s the authors of Dark Moon concluded that the photo below is an example of such an image. This finding was the result of shadow analysis of all the rocks compared with the anomalous shadow of the LM in this picture. The conclusion was that as the scene was illuminated by an artificial light source, impossible on the Moon, the image must have been photographed on a studio set with full control of the scene and the lighting.
 Apollo 14 AS14-68-9486 |
Natural sunlight cannot result in the shadow divergence seen in AS14-68-9486. Moreover, while the foreground rocks have dense shadows rendering part of these objects totally black, detail is still visible on the shadow side of the LM (and the astronaut). The finding that 'unnatural' lighting must have been deployed has been challenged by various individuals over the years, including the Principal Image Quality Engineer at NVIDIA, USA Robin Jenkin.1 In AS14-68-9486 the foreground rocks appear to be on a slight rise relative to the rest of the scene. This minor difference in terrain levels is often cited as the reason for the considerable shadow divergence.
A closer inspection reveals that all the rock shadows in this image are consistent with illumination from the same light source. The key to this understanding lies within rectangle (a). Even these rocks in the mid ground have shadows falling in a direction that is consistent with the primary light source. It is only the intruders in this particular lunar landscape – the LM, the flag (and as we shall see, the astronaut) – which have shadows caused by a different, ’secondary’ light source.
 Close up of rocks in rectangle (a) in the background of AS14-68-9486 |
This shadow divergence had been noted by plasma physicist, and expert in the technique of ray tracing, Luis Bilbao. He contacted Aulis after studying this Apollo 14 image pointing out that shadow directions alone are insufficient to establish the presence of more than one light source (or the location of the source of lighting). At our request he kindly agreed to write up his ray tracing results for publication on Aulis Online.
The following is the short paper by Luis Bilbao, Adjunct Professor and Independent Researcher, INFIP CONICET, UBA, Argentina.
Ray Tracing an Apollo 14 Photograph
Luis E. Bilbao, PhD
Introduction
Numerous Apollo lunar surface photographs as published by NASA are considered to have been adjusted or manipulated. Why have these images been manipulated? Some people believe it is good practice to improve these photographs. But this practice is not acceptable to either the student or the public, let alone to scientists. As any such manipulation casts doubt on the entirety of the Apollo project it is therefore perfectly legitimate to scrutinize all the available material from these missions.
The main scope of this paper is to analyse an image from Apollo 14. Shadows as reproduced in a photograph are a projection of a 3D phenomenon into a 2D plane that sometimes creates counter-intuitive results. Today there are many software applications that can reproduce the shadow pattern of a model. However, by applying very simple simulations (even using a spreadsheet) it is possible to demonstrate that there are no reliable grounds – based on shadow directions alone – to assert whether or not more than one light source is present in any given Apollo lunar surface picture.
Shadow direction
 Figure 1: Sample shadows produced by the sun on vertical parallel objects. Parallel shadows appear to converge in a 2D photograph |
Consider a simple example of parallel vertical objects as depicted in Fig.1. Although the shadows are actually parallel on the floor, their 2D projection manifests as convergent shadows (towards a vanishing point). The same situation on an irregular terrain may produce even more distorted shadows in a photograph.
A quoted example of incorrect shadow directions is AS14-68-9486, Fig.2.
 Figure 2: AS14-68-9486, with the shadow direction of the foreground and background objects indicated by red arrows |
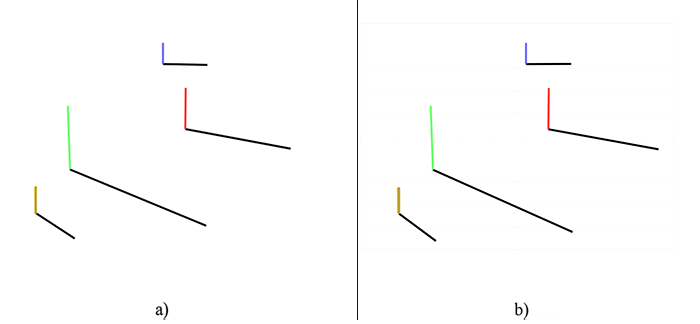
 Figure 3: Simple setup of four vertical sticks (blue, red, green and brown) on a planar surface, as seen from above. The blue stick is further away relative to the other sticks. A camera is located at (0,0) |
This pattern can be understood using the following example (Fig.3). An arbitrary unit is used – it may also be read as meter. Consider four straight vertical sticks on a planar surface located at coordinates: blue stick (1;110), red stick (0.5;11), green stick (-1;7), and brown stick (-1;5). The heights are 5, 1, 1, and 0.3, respectively. A camera is located at (0;0). A unique light source is located at 30 degrees from positive y direction, and 20 degrees of elevation. A simulated image of the corresponding shadows is shown in Fig. 4 using two different distances for the light source: a far one (100,000) and a near one (100).
|
The difference is hard to see using this simple sticks configuration on a planar surface. Note that the angle between the blue and the green shadows does not differ much from the shadow angles of the Apollo image, in Fig.2 above.
Shadow analysis is therefore not the best way to determine whether or not more than one source of light is present in photographs where the terrain is irregular and object separation may be quite large. A better approach and a far more powerful and reliable method is to deploy the technique of ray tracing. Light rays are straight lines in both the 3D world and on the 2D image plane. They do not depend on the shape of the terrain and can be extended even beyond the objects.
Method of light ray tracing
In a uniform medium, light propagates in a straight line. Rays from a distant source are parallel and they do not cross each other. But, their projection on the film surface may appear to be convergent. Although not visible, it is possible to follow the direction of a ray by identifying point couples that belong to them. For example, with an illuminated point and its corresponding shadow. In what follows, the term ‘ray’ will refer to the direction of light propagation that includes the region to where the light actually propagates and the region beyond opaque bodies.
Rather than going through the mathematics, I will show how to trace the rays and to describe some information that can be extracted from them. Consider again the sample shadows of Fig.1, where several couples of associated points are marked as in Fig.5.
 Figure 5: Some points and their corresponding shadows (marked as 1-1 left door sticker; 2-2, right door sticker; and 3-3 right door frame), each couple belonging to a ray (as will be seen in Fig.6) of the sample photo in Fig.1 |
Distinctive points should then be used for ray tracing, as with the marked pairs 1-1, 2-2 and 3-3. By joining these points, the rays (technically, their projection on the film) are drawn as straight lines that can be extended back to their convergence point, Fig.6.
 Figure 6: Ray tracing on the photographic plane from points defined in Fig.5 with the camera in this case held at the photographer's eye level |
Note that the convergent point of these rays on the film plane coincides with the position of the shadow of the camera. This is not surprising because all rays converge to a unique point, and the projection of the ray joining the camera and its shadow is represented by a point on the film. If a trajectory is represented by a point, then this point should also be the point of convergence. Figs.7 and 8 show the convergence point for different camera positions.
 Figure 7: Ray tracing, convergence point and camera location at chest level of the photographer |
 Figure 8: Another example with the convergence point and camera location held above eye level of the photographer |
The ray tracing technique has the added advantage of being independent of the terrain contours. As long as a point and its corresponding shadow can be determined, the ray is easily constructed because those points belong to a ray. This technique produces some interesting results: a) if a unique source of light is present, all rays converge to a unique point, b) if the source is behind the camera, and its shadow is present in the photo, then the convergence point coincides with the shadow of the camera, c) if the source is in front of the camera, then all rays converge towards the source.
 Figure 9: AS16-108-17627. A couple of distinctive points are chosen for ray tracing |
An example is shown in image AS16-108-17627, (Fig.9). The shadows are well defined allowing the determination of some point couples, marked as 1-1 the ‘stick’; 2-2, the paper held by the astronaut and 3-3 the astronaut. The rays converge to a unique point that should coincide with the shadow of the camera, since the sun is behind the camera, see Fig.10.
 Figure 10: AS16-108-17627. Ray tracing (in yellow), indicating that only one light source is present – but that in this case, the camera is not mounted on his chest bracket but is located in the area of the head of the astronaut |
On a planar terrain, the intersection of the shadow directions occurs at the natural horizon (H). However, in this photo the intersection point is much closer than the natural horizon (see Fig.11) indicating that either the astronauts are in a lower part of the terrain or that the light beam is convergent. The intersection point of the shadows defines the local horizon – a notional horizontal line crossing through the intersection point of the shadows.
Then, the local elevation of the light source can be easily determined by measuring the angle between the local horizon and the intersection point of the rays. To do this also requires knowledge of the focal length of the camera lens together with the actual dimensions of the recorded film image – information readily available from the Apollo photographic record.
 Figure 11: AS16-108-17627. Shadow directions (in red) intersect in the middle distance, indicating that either the astronauts are in a lower part of the terrain or that the light beam is convergent |
Finally, consider the example of the Apollo 11 composite image AS11-40-5863-69 by Ed Hengeveld, composed of photos AS11-40-5863 to 69, plus AS17-149-22860 (used for the antenna), see Fig.11a below. By tracing some of the rays, it is evident that the ‘sun’ is incorrectly positioned. This is confirmed by the fact that the rays converge to a different place in the image. According to the image compositor Ed Hengeveld, “the 'sun' is a Photoshop effect that I placed approximately where the sun would be in the sky.” Clearly, Mr Hengeveld is unaware of the direction of the rays in the image, otherwise it is likely that he would have placed the 'sun' in a more realistic position.
 Figure 11a: Lunar Module "Eagle" composite by Ed Hengeveld. An image comprising AS11-40-5863-69, plus AS17-149-22860 (used for the antenna) published by NASA. Rays converge to a location that does not correspond to artificially-added ‘sun’ in the sky |
Analysis of photo AS14-68-9486
 Figure 12: Photo AS14-68-9486. Some characteristic lengths (blue lines) and several ray segments (yellow lines) formed from a point in an object and its shadow – Click to enlarge |
I present here a first analysis of photo AS14-68-9486 (Fig.12), performed through the following steps: a) determination of characteristic lengths for calibration purpose, b) search for point couples that belong to a ray (an object point and its shadow) to form ray segments, c) using as many segments as possible to determine the source position (in the plane of the film), for example, by means of a least square technique, d) tracing rays from the source to the objects where the segments were determined, e) search for outliers, in order to remove and recalculate the source position, and f) search for any incompatibility between ray paths and shadows.
Shadow segments and light rays
In Fig.12 several characteristic lengths and/or directions are plotted as blue lines. The height of the astronaut, the LM, and the flag mast are highlighted. Taking into account the separation of the fiducials (crosshairs) (10 mm) and the focal length of the camera lens (60 mm), the LM should be at a distance of (81.1±2.7) m away from the camera.
Assuming a mostly planar terrain, the rocks inside the black rectangle (see Fig.12a) should be located only several meters closer to the camera than the LM. Notwithstanding this, it can be observed that the shadows produced by the rocks point in a totally different direction to those of the LM, which could indicate the presence of more than one light source.
A study using ray tracing can be the means to test the likelihood of this being correct. Several segments (yellow lines) belonging to different rays are also shown in Fig.12, numbered from 1 to 12: there are 10 from the rocks plus 1 from the flag and the other from the LM.
 Figure 13: Least squares method used to determine the position of the light source |
In order to determine the position of the source a least squares procedure is used. Since the problem is non-linear, a good initial guess is needed, which can be obtained by simple inspection. A rough ray tracing will define an area where the solution will probably be found. From a position within this area the minimum angle between the direction to a point and the corresponding ray segment is sought. In practice the summation over all the square angles is used.
The best fit corresponds to a source located at 1150.5 pxl away from the left border, and 635.2 pxl above the top border. Once the source position is determined, it is possible to trace the rays. The angular deviation of the segments relative to the rays emanating from the source are plotted in Fig.13.
 Figure14: Result of ray tracing the image. The orange circle indicates the best fit for the position of the light source, surrounded by an ellipse which defines the region where the source is most probably located. The magenta dashed line is the prolongation of the LM segment showing that an extra source of light is needed to explain its shadow – Click to enlarge |
The positive values indicate a counter-clockwise rotation. Clearly, both the flag and the LM segments are not well fitted. They deviate by more than 6 deg, a number that in the present analysis is statistically different from zero. Whereas the mean value over the rock segments is (0.13±1.30) deg – indicating that the fit is excellent.
Taking into account the dispersion of the angle of the rock segments, the most probable region from which the light source emanates is shown in Fig.14 as an orange ellipse. This surrounds the orange circle that corresponds to the best source position, as mentioned above. The dotted magenta line shows that the direction of the LM segment does not overlap the orange ellipse, thus requiring an extra light source to explain its shadow.
Note that the ellipse is very elongated in the direction of the rays. This is a phenomenon similar to that known in GPS as the geometric dilution of precision (GDOP). This occurs when most of the satellites are confined in a reduced part of their space (i.e., they are almost aligned). However, this phenomenon cannot explain the angular deviation of the LM segment, because its prolongation lies well away from the ellipse.
In Fig.15 a detailed view of the rays corresponding to the shadow segments are plotted as green lines. As can be seen, the rays and the segments for the rock shadows are well aligned. The segments corresponding to the LM and the flag are clearly tilted relative to the rays coming from the primary source, indicating that light is coming from another source or from an extended source. Another anomaly is the absence of the astronaut’s shadow where it should be located. A parallel line to the LM segment is traced from the top of the astronaut’s suit, represented by a dashed yellow line. The region between this line and the light ray (green line) is where the shadow is expected to be, see the blue ellipse in Fig.15.
 Figure 15: Closer view of the rays emanating from a point-like source located at (-1150.5;635.2) relative to the left top border of the image – Click to enlarge |
Further observations
It is interesting to check further the ray propagation and shadows in other objects other than the ones used for the determination of the source position. In Fig.16 the detailed ray tracing (green lines) around the bottom right corner is shown. Additionally, blue arrows are added to indicate the point on an object and its corresponding shadow. A very good fit is observed here also.
 Figure 16: Close-up detail of the ray tracing (green lines) in a region close to the right bottom border. Blue arrows indicate a given point in the object and its corresponding shadow |
Finally, by increasing the brightness and contrast of the photograph, several light traces become more visible on the dark sky area – see Fig.17.
 Figure 17: Increased brightness and contrast reveals some light traces mainly visible against the dark sky and the large circular flare |
Besides the large circular flare, (produced when light from a source directly reaches the front element of a camera lens reflecting and bouncing off different lens elements) there are also several visible rays present in the image – often described as a sunburst or starburst effect. One possible explanation for these rays is based on a possible obstruction in the optics, in particular, by the camera’s aperture blades. When a bright light hits the camera lens it can produce these kinds of artifacts. In the case of this Apollo 14 photo, the number of ‘spikes’ or star points is dependent on the number of the aperture blades (the iris) in the lens (see Fig.19) and the orientation is just the orientation of the camera.
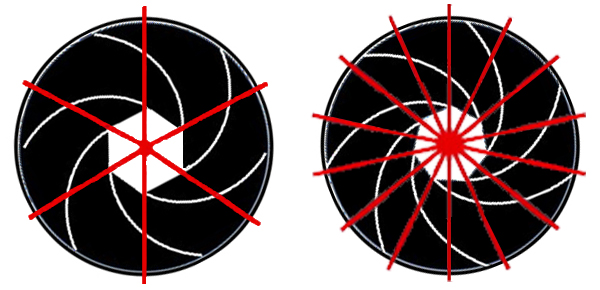
 Figure 18: AS11-36-5293, illustrating the star point artifacts produced by the aperture blades in the camera lens when an intense light source hits the objective of the lens. This camera would have had a five-bladed aperture |
This Starburst effect is most noticeable when a lens is stopped down to an aperture between f/11 and f/22. It is also relative to both the lens used and varies according to the number of aperture blades within the lens. Different lenses produce different results. If the camera lens has an even number of blades it will produce the same number of star points as there are blades. And if it has an odd number of blades, it will result in double the number of star points as there are blades, see Fig.19 below.
|
But in the present case of the Apollo 14 image, these rays do not appear to be uniformly distributed, nor do the numbers accord with the number of aperture blades. Curiously, the observed light traces are perfectly aligned with the rays from the source, see Fig.20. The question is what are they in reality? Are they a result of an aperture obstruction? Or are they rays that exist because they are propagating through a medium? Lunar dust suspended in the ‘air’? In this case, the presence of particles (say an atmosphere) is necessary in order to explain them.
 Figure 20: Light traces are perfectly aligned to the rays emanating from the source |
Conclusions
In the case of photo AS14-68-9486 a simple analysis of shadow directions alone is not enough to reach an objective conclusion regarding the presence of more than one light source, nor the divergence (or convergence) of the light beam. It is advisable to use the additional technique of ray tracing. Application of the ray tracing technique is more powerful than one based on shadow directions. By using 12 ray segments from the shadows produced by the rocks and the LM it is possible to determine the position of the light source.
Then by drawing the rays emanating from the source, it is possible to check whether or not a given shadow in the image is compatible with the presence of a point-like source. Of course, further careful analysis, which includes more ray segments could be conducted, in order to decrease the uncertainty of the source location and to discriminate, beyond the error limits, the shadows that are incompatible with a unique point-like source. Additionally the appearance of flares and rays could studied further.
Luis E Bilbao
Aulis Online, July 2018
Note: Due to their large size, photographs are not optimised for viewing on cell phones
About the Author
Luis Ernesto Bilbao has a PhD in Physics from the University of Buenos Aires, is Adjunct Professor, and Independent Researcher, INFIP CONICET, UBA (the Faculty of Exact and Natural Sciences, University of Buenos Aires, Argentina).
The Institute of Plasma Physics (INFIP), dependent on the CONICET and the FCEyN-UBA, is a center carrying out pure and applied research in a wide variety of subjects of this discipline. The INFIP researchers have extensive knowledge and many years of experience in this branch of physics, with the publication of more than 600 works since 1983.
Footnote
1. “Photographic Anomalies of the Apollo Space Programme” Dr. Robin Jenkin, Portfolio One, RPS, 2007.
Dr Robin Jenkin is also a Visiting Professor, University of Westminster, London.
See the article NVIDIA: Mission Failure, Aulis Online.
And also Examples of anomalies and inconsistencies in the Apollo photography, Aulis Online.
AULIS Online – Different Thinking